High-Resolution Image Synthesis with Latent Diffusion Models
TL;DR
本文提出一种DM(diffusion mode)的改进模型,称为latent diffusion model, 在图像合成和其他领域取得了极高的效率和性能。原始的DM模型直接在像素空间操作,训练需要数百个GPU小时且推理时需要顺序执行。为了在训练资源有限的条件下维持高性能,本文讲DM应用在一个预训练自编码模型的latent space里。这样的表达方式在计算量缩减和维持细节两方面实现了比较好的tradeoff。 通过引入cross-attention,作者把扩散模型变成对一般条件输入(文本or bounding box),并且可以通过卷积方式实现高分辨率合成。

- 不那么激进的下采样,可以提升质量的上界。
Method
- 避免高维度图像的上计算之后,扩散模型的计算更加高效。得到的通用压缩模型的潜在空间可以用来训练多个生成模型,并且也可以用于其他下游应用,例如单图像CLIP引导的合成。
Perceptual Image Compression
- 感知压缩模型由自编码器构成,训练时采用perceptual loss 和 patch-based 对抗loss
- 为了避免在latent space 上出现高维的方差,作者使用了两种正则化方式:(1)KL正则化,使latent space 空间更加趋向于正态分布 (2)VQ-reg, 向量量化正则化,在解码器中使用了VQ层,这部分模型可以当作VQGAN。该模型的DM部分是为了处理二维结构的潜在空间,这和之前的1d 潜在空间是不同的,作者认为这样能更好的保持内在结构
Latent Diffusion Models
Diffusion model
- DM 被建模成概率模型,通过逐渐对一个正态分布的变量进行降噪,从而学到数据分布p(x)。这个逐渐降噪的过程对应固定的马尔可夫链的逆过程。
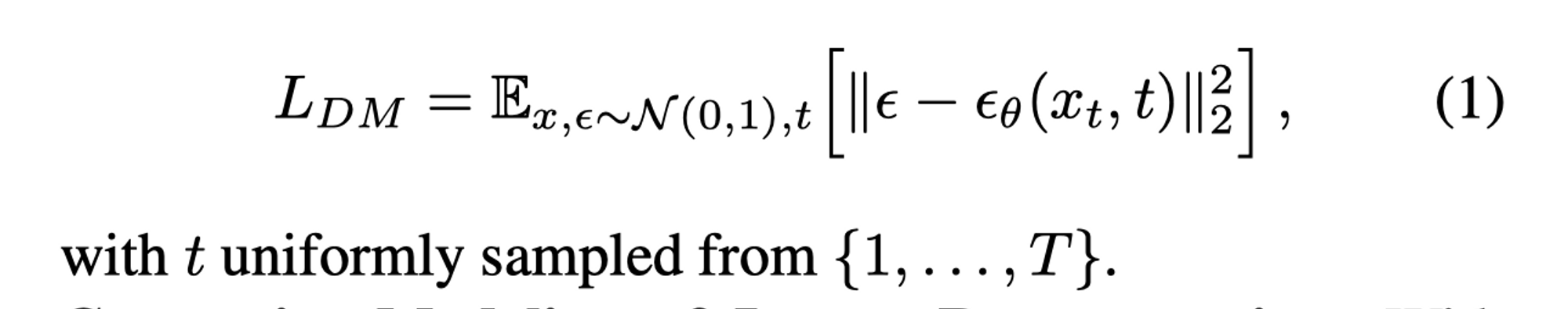
- 对所有的训练图像 x,噪声分布ǫ(服从标准正态分布N(0,1)),和扩散步骤t,计算噪声和模型预测的去噪版本 $\epsilon_{\theta}(x_t, t)$ 之间的欧氏距离的平方(即 L2 范数的平方),然后对所有的 $\epsilon , \theta , {t}$ 求期望。这个期望的计算可以通过在训练数据上进行平均来实现。
Generative Modeling of Latent Representations
- 在潜在空间里,所有的抽象高频信息都被抽离。相比高分辨率空间,这个空间更适合进行似然的生成模型。有两点好处(1)专注于数据相关,语义相关的信息 (2)在一个计算效率更高的维度进行训练。
- 和一些基于注意力的Transformer, 潜在空间压缩,离散自回归模型不同. 可以更好的使用针对图像的归纳偏差,这包括使用2D卷积层构建底层UNet的能力,以及通过重新加权边界进一步将目标集中在视觉上最相关的位上。
- latent diffusion 中的Unet 是time-condition的,是希望不同时刻的T能处理不同时刻的噪声,它的权重也应该是随着t变化的。
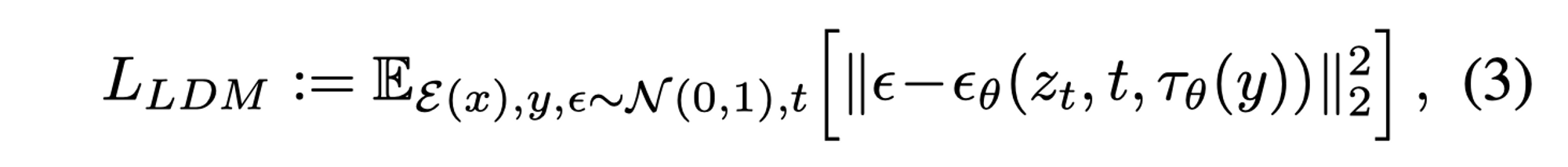
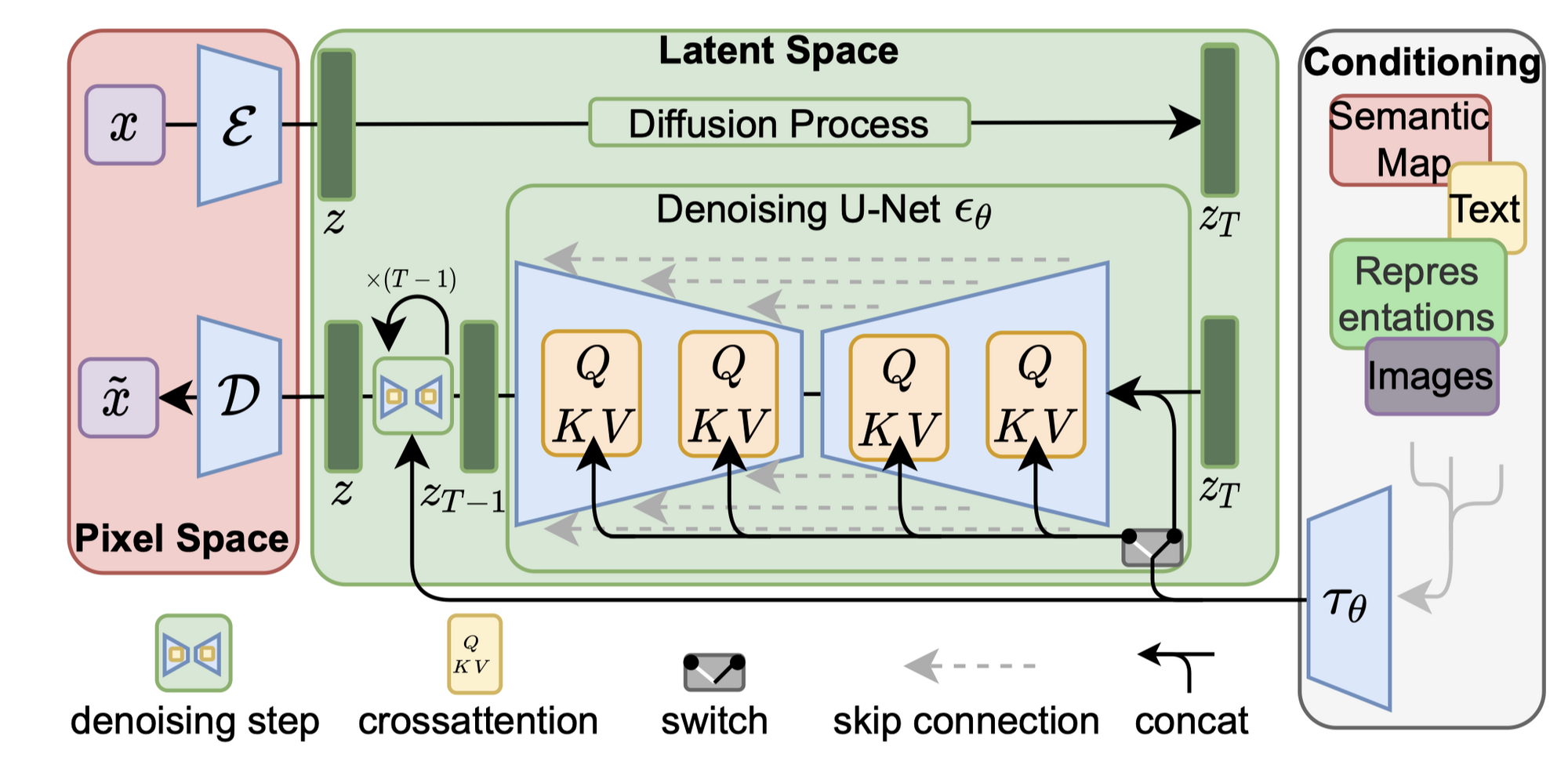
- 为了处理多模态数据,还是使用了cross-attention 方法:
$$
Attention(Q, K, V) = Softmax(\frac{QK^T}{\sqrt{d}})V
$$
其中$Q=W_Q^{(i)} * \varphi_{i}(z_t)$ , $K=W_K^{(i)} * \tau_{i}(z_t)$, $V=W_V^{(i)} * \tau_{i}(z_t)$ 。
- $\varphi_{i}$ 表示Unet 处理后再经过flatten 的向量
- $\tau_{i}$ 表示表示对多模态进行融合的网络